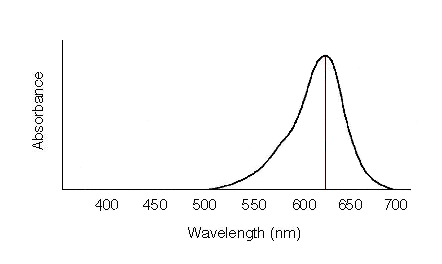
This sample absorbs in the orange region, so the transmitted color would be blue.
Last updated 06/30/05 12:52 PM
Objective
In this experiment, the equilibrium constant will be determined for the formation of a complex ion, [Fe(H2O)5(SCN)]2+. This will be accomplished by using a Spectronic-20 Colorimeter to measure absorbance data, from which equilibrium concentrations can be calculated with the Beer-Lambert Law, A = e l c.
Introduction
When continuous electromagnetic radiation (light) passes through a material, a portion of the light may be absorbed. The remaining light exits the sample and, when passed through a prism, will yield a spectrum with gaps in it. This is called an absorption spectrum. The color that our eyes see is due to the wavelengths of light that the sample did not absorb, that is, we see the transmitted color. For example, if a sample solution absorbs light in the orange region of the spectrum, the solution will appear blue to our eyes. A color wheel can be used to relate absorbed and transmitted colors. The transmitted color is opposite the complementary color of the absorbed light. The relative intensity of color is proportional to the concentration of the dissolved compound. The greater the compound's concentration, the darker (more intense) the solution color appears.
 |
lmax = 625 nm
This sample absorbs in the orange region, so the transmitted color would be blue. |
When atoms and molecules absorb energy they pass from a state of low energy (ground state) to a state of higher energy (excited state). This excitation process is quantized and the absorbed energy always exactly equals the energy difference between two energy levels in the atom or molecule. A typical solution absorption spectrum for a compound absorbing in the visible region of the electromagnetic spectrum is shown above. Wavelengths in the visible spectrum range from approximately 350 nm to 700 nm. The point of maximum absorbance corresponds to the energy difference between two energy levels unique to the compound. In the illustration above, the wavelength of maximum absorbance (lmax), occurs at approximately 625 nm, which can be converted to energy using the relationship E = hc/l. The focus today is not on energy levels, but on the relationship between concentration and intensity of color exhibited by an absorbing species. This relationship will be used to calculate the equilibrium concentrations and the equilibrium constant, K.
A quantitative relationship exists between the amount of light absorbed at each individual wavelength and the concentration of the substance dissolved in a given solvent. This relationship is known as the Beer-Lambert Law (or Beer's Law), A = e l c, where A is the measured absorbance of a solution, e is the molar absorptivity constant (M-1cm-1), l is the cell path length through the solution (usually 1 cm), and c is the concentration of the solution (M). The molar absorptivity constant has a unique value at each wavelength of the spectrum of a solution. If a solution of compound obeys the Beer-Lambert Law, a plot of absorbance at a given wavelength vs. concentration give a straight line with a slope of e·l. (Recall that the equation for a straight line is y = mx + b.) In this case, y is the absorbance and x is the concentration. The y-intercept (b) is zero, since the line will pass through the origin of the graph. The first task of the following lab report will be to plot given absorbance and concentration data to determine the molar absorptivity constant value. Once this value is known, you will be able to calculate equilibrium concentration values from the measured absorbance values for your sample. Again, the underlying concept is that concentration is directly related to absorbance.
The relationship between absorbance (A) and percent transmittance (%T) is also quantitative. The light entering the sample is called the incident light and its intensity is designated as Io. The light which leaves the cell is the transmitted light and its intensity is designated as It. Transmittance is defined as the ratio It/I0. Percent transmittance is It/I0 x 100. Absorbance equals log(Io/It) or -log(%T/100). Both A and %T can be obtained directly from the Spectronic-20 colorimeter.
Operation of the Spectronic-20
The Spectronic-20 is the instrument with which the absorbance values will be measured. Click here for a picture. Most Spec-20's have an analog meter dial on which both absorbance and % transmittance can be measured. Newer models have a digital display which can be changed to read either. A wavelength knob is available to adjust the wavelength setting. This is usually set to lmax. The sample compartment (or sample holder) uses a special cuvet, which looks like a small test tube with a vertical line on one side. This line is aligned with a raised line under the sample holder cover. This alignment ensures that the cuvet is placed into the holder in exactly the same position each time. This helps to minimize the variation that may exist in glass thickness and imperfections in the cuvet diameter. These cuvets must be internally clean and free of external dirt and fingerprint smudges. A Kimwipe is used to wipe the outside just before placing into the holder. You should fill the cuvet about 3/4 full with solution. The blank usually contains a solvent or some other standard and is used to zero the instrument before taking absorbance measurements. The zero-adjust knob is located on the left front, and the 100% Transmittance knob is on the right front of the instrument. The instrument should be warmed up for at least 15 minutes prior to use.
Absorbance and the Equilibrium Constant, K
The equilibrium reaction between Fe3+ and SCN- will be studied today, which is represented in aqueous solution by the following reaction. The [Fe(H2O)5(SCN)]2+ ion produces a red-orange solution.
[Fe(H2O)6]3+ + SCN- <==> [Fe(H2O)5(SCN)]2+ + H2O
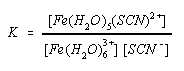
As with any equilibrium, the value of K will be the same regardless of the initial concentrations of Fe3+ and SCN-, as long as the temperature is constant.
Seven solutions will be prepared from different initial concentrations of Fe3+ and SCN-. Upon mixing the two reactants, equilibrium is established almost instantaneously. Each solution will have a different measured absorbance value. These absorbance values will be converted to concentration using Beer's Law. This concentration will be the equilibrium concentration of [Fe(H2O)5(SCN)]2+ present in each sample. Knowing the initial concentrations of the reactants and the equilibrium concentration of the product, you can calculate the equilibrium concentrations of the reactants. You will then calculate the value of K by placing the equilibrium concentration values into the equilibrium constant expression. Please see the table of reaction concentration values (M) below.
Table of Reaction Concentrations
| [Fe(H2O)6]3+ | SCN- | [Fe(H2O)5(SCN)]2+ | |
| initial (i) | A | B | 0 |
| change (D) | - x | - x | + x |
| equilibrium (eq) | A - x | B - x | x |
Procedure
| Stock solutions: | 0.00200 M Fe(NO3)3 - produces
[Fe(H2O)6]3+ (or simply Fe3+)
in solution 0.00200 M KSCN - produces SCN- in solution |
Clean and rinse eight medium test tubes. Prepare the seven solutions with volumes of reagents as given in the table below. The eighth sample will be used as the "blank" for zeroing the Spec-20. Use a 5-mL serological pipet to measure the solutions. A serological pipet is graduated so that more than one volume measurement can be made with the same pipet. Measure the volumes accurately. Note that the total volume in each sample is 10.00 mL. Be sure to keep the test tubes in order. You should notice an increase in the intensity of the observed color as more SCN- is added and, thus, a higher concentration of [Fe(H2O)5(SCN)]2+.
| CAUTION: | These reagents are dissolved in 0.50 M nitric acid (for stability). Wash hands or other areas immediately if any is spilled. |
Volume Table (All volumes are in mL.)
| Sample # | Fe3+ | SCN- | distilled H2O |
| 1 | 5.0 | 1.0 | 4.0 |
| 2 | 5.0 | 2.0 | 3.0 |
| 3 | 5.0 | 3.0 | 2.0 |
| 4 | 5.0 | 4.0 | 1.0 |
| 5 | 5.0 | 5.0 | - |
| 6 | 2.5 | 5.0 | 2.5 |
| 7 | 3.5 | 5.0 | 1.5 |
| blank | 5.0 | - | 5.0 |
Spectrophotometric Determination of [Fe(H2O)5(SCN)]2+
Spectrophotometric measurements will be made using a Spectronic-20 Colorimeter. Use the same instrument for all absorbance measurements. Set the instrument wavelength control to 447 nm and zero the instrument (instructions below) using a cuvet containing the blank solution. Empty the cuvet, rinse with distilled water, and shake dry. Next, fill the cuvet with Sample #1, insert the cuvet and read the absorbance value. Record the absorbance value. Discard the first sample, rinse the cuvet with distilled water and proceed in the same way with the other six samples. When all absorbance values have been recorded, discard all samples and rinse the cuvet and test tubes with distilled water.
To calibrate or "zero" the Spectronic-20:
An animated version of the instructions above is available here. Thanks to Carol Ann Paul of Wellesley University.
Report
You are to design your own data tables and concentration tables for this report. It is strongly recommended that you use a spreadsheet for these tables, from which your results can be printed directly. Label your tables appropriately and completely.
1. Calibration curve (to be completed as a part of the pre-lab)
In order to convert your measured absorbance values to concentration (M), a calibration "curve" must be constructed to find e, the molar absorptivity value. Use the following data to plot Absorbance vs. Concentration (M) of [Fe(H2O)5(SCN)]2+. Determine the slope of the line, which equals e·l, as described above in the introduction. The cell path length (l) equals 1 cm. Thus, the slope equals e, the molar absorptivity value.
Concentration (M) of [Fe(H2O)5(SCN)]2+ Absorbance 3.0 x 10-5 0.147 6.0 x 10-5 0.308 9.0 x 10-5 0.462 1.2 x 10-4 0.612 1.5 x 10-4 0.764
Note: The absorbance values were updated on Monday, March 12, 2001.
Clearly identify your molar absorptivity value with appropriate units.
2. Table of measured absorbance values and their corresponding concentration values.
List your measured absorbance values for each sample. Convert absorbance to concentration using your value of e (from part 2) and Beer's Law. These calculated concentration values represent the equilibrium concentrations of [Fe(H2O)5(SCN)]2+, which is labeled as x in the table referred to in Part 4.
3. Table of initial concentration values.
Utilizing the concentrations of the Fe(NO3)3 and KSCN stock solutions, the volumes of each solutions used, and the total volume of each sample, calculate, using M1 V1 = M2 V2, the initial concentrations of [Fe(H2O)6]3+ and SCN- for each sample. These are labeled as A and B, respectively, in the table referred to in Part 5.
For example, if 6.0 mL of 0.002 M Fe(NO3)3 were used and the total sample volume was 10.0 mL, the concentration would equal (6.0 mL)(0.002M)/10.0 mL or 1.2 x 10-3 M.
4. Table of reaction concentration values
Complete a table of reaction concentration, like that above in the introduction. Plug in values of A, B, and x calculated from previous parts above to calculate the equilibrium concentrations of [Fe(H2O)6]3+ and SCN- for each sample.
5. Equilibrium constant, K, values
Use the equilibrium concentrations from Part 5 for each sample to calculate an equilibrium constant for each sample. Compute the average K value and include a standard deviation.
6. Questions
[Fe(H2O)6]3+ + SCN- <==> [Fe(H2O)5(SCN)]2+ + H2O
What if the the actual equilibrium reaction was the following?
[Fe(H2O)6]3+ + 2 SCN- <==> [Fe(H2O)4(SCN)2]2+ + 2 H2O
Given that the experimental data of this experiment are as obtained, would the equilibrium concentrations of the reactants or product change? Justify your answer.
How would this change the equilibrium constant value, K, if the initial volumes and concentrations were the same as for the lab as performed? Note that 2 moles of SCN- are required according to the equation.